Безье

Cтраница 1

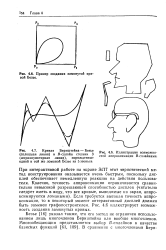
Безье объясняется существенно большей простотой написания соответствующих программ ЭВМ по сравнению с программами, реализующими более совершенные методы построения кривых по точкам. [1]

Безье расположен внутри выпуклой оболочки множества точек-ориентиров. [2]

Безье совпадает с последней точкой определяющего многоугольника. [3]

Безье ( 1970) перегруппировал члены параметрического кубического многочлена Фергюсона таким образом, что физический смысл векторных коэффициентов стал более ясным. [4]

Безье ( 1970) показывает, что этот метод нахождения точки можно распространить на кривые высокого порядка, записанные в форме Бернштейна - Безье. [5]

Безье, остается внутри тетраэдра, вершины которого являются точками характеристической ломаной этой кривой. Подобным же образом можно показать, что сегмент конического сечения остается внутри треугольника Р Ра при 0 и 1, если веса имеют положительные значения. [6]

Безье, прямых линий и кривых произвольной формы. [7]

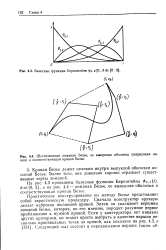Базисные функции Бернштейна q, ( t, k e.| Шестизвенная ломаная Безье, ее выпуклая оболочка ( штриховая линия и соответствующая кривая Безье. [8]

Безье, ее выпуклая оболочка и соответствующая кривая Безье. [9]

Пример создания замкнутой кривой Безье.| Кривая Бернштейна - Безье ( сплошная линия и В-сплайн степени 3 ( штрихпунктирная линия, порожденные одной и той же ломаной Безье из 5 звеньев.| Иллюстрация возможностей аппроксимации В-сплайнами. [10]

Безье [16] указал также, что его метод не ограничен использованием лишь многочленов Бернштейна или вообще многочленов. [11]

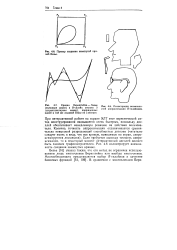
Тоновые поверхности, построенные с помощью густой сетки линий ( затенение выполняется путем управления током луча.| Генерация поверхности методом Безье. [12]

Безье для случая двух переменных; б - соответствующая бикубическая поверхность. [13]

Безье [16] указал также, что его метод не ограничен использованием лишь многочленов Бернштейна или вообще многочленов. [15]

Страницы: 1 2 3 4 5