Безье
Cтраница 3
Кривая Безье ( Buzier curve) - параметрическая кривая, определяемая группой полиномов третьего порядка с четырьмя управляющими точками. Кривые Безье удобны для изображения плавно изменяющихся пространственных объектов типа изогипс и водотоков. Кривые Безье также используются для размещения названий вдоль извилистых объектов, таких как реки. [31]
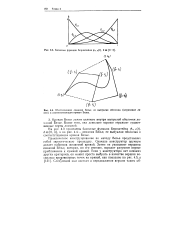 |
Базисные функции Бернштейна р, i ( t, и е.| Шестизвенная ломаная Безье, ее выпуклая оболочка ( штриховая линия и соответствующая кривая Безье. [32] |
Кривая Безье лежит целиком внутри выпуклой оболочки ломаной Безье. Более того, она довольно хорошо отражает существенные черты ломаной. [33]
Метод Безье для интерактивного конструирования кривых может быть легко распространен на случай конструирования свободных поверхностей. [34]
Кривая Безье ( Buzier curve) - параметрическая кривая, определяемая группой полиномов третьего порядка с четырьмя управляющими точками. Кривые Безье удобны для изображения плавно изменяющихся пространственных объектов типа изогипс и водотоков. Кривые Безье также используются для размещения названий вдоль извилистых объектов, таких как реки. [35]
Кривые Безье, дуги окружности, эллиптические дуги н линии являются тигимн сегментов, которые, будучи соединены в конечных точках, образуют пути. [36]
Сегмент Безье кубической кривой, введенный в разд. [37]
Содержательно многочлен Безье можно представить как некоторую намагниченную эластичную ленту, закрепленную в первой и последней точках; во всех остальных точках размещены магниты. При стремлении кратности к бесконечности многочлен Безье стремится к ломаной кривой, точками сопряжения для которой служат точки-ориентиры. [38]
Определить кривую Безье, используя координатные векторы, заданные в примере 5 - 2, как определение многоугольника. [39]
Сгенерировать поверхность Безье из примера 6 - 14, не используя матричных методов. [40]
 |
Кривые Безье Смещение Размер Описание.| Атрибуты графического текста Смещение Размер Описание. [41] |
Изображение кривой Безье использует текущие атрибуты линии. Не поддерживается в WP 5.0; для переносимости также включает аппроксимацию изображения при помощи ломаных линий. [42]
 |
Характеристический многогранник порции кубической поверхности. [43] |
Кубические кривые Безье, как упоминалось ранее в разд. Фергюсона, заданные в такой форме, что не требуется определения каких-либо касательных. Существует такая же тесная связь между порциями поверхностей, заданными в форме Фергюсона и Безье. Безье проектируется с помощью характеристического многогранника, который определяется векторами положения rif его 16 вершин. [44]
Нарисовать кривую Безье, проходящую через данные точки. [45]
Страницы: 1 2 3 4 5