Неустойчивость - движение
Cтраница 2
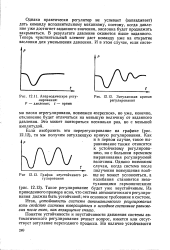 |
Апериодическое регулирование. Р - давление. t - время.| Затухающая кривая регулирования. [16] |
Понятие устойчивости и неустойчивости движения системы автоматического регулирования решает вопрос, имеется или отсутствует затухание переходного процесса. [17]
Первая теорема Ляпунова о неустойчивости движения. [18]
Важно заметить, что неустойчивость денежного движения в немалой мере обусловлена двумя ранее рассмотренными противоречиями макроэкономики. [19]
В случае п 1 наблюдается неустойчивость движения. Случай г г подтверждает это заключение. [20]
В случае п 1 наблюдается неустойчивость движения. Случай г0 г подтверждает это заключение. [21]
Ляпунову принадлежат две теоремы о неустойчивости движения. В 30 - х годах нашего столетия Четаев обобщил эти теоремы и доказал теорему, из которой как частный случай вытекают теоремы Ляпунова. Поэтому мы начнем с изложения теоремы Четаева. [22]
Автор отмечает, что помпаж - неустойчивость движения - проявляется в форме колебания всей массы среды, заполняющей машину и сеть, и что частота колебаний существенно зависит от инерционности, а амплитуда - от демпфирующих свойств системы. [23]
Рейнольдса, при котором возможно возникновение неустойчивости движения. Однако в подобных расчетах, как правило, не учитывается зависимость основных теплофи-зических свойств и в первую очередь вязкости расплавленной жидкости от температуры. [24]
Второй, переходный, режим характерен неустойчивостью движения, появлением локальных разрывов плотного слоя по длине и периметру канала. [25]
Вторая категория возможных колебаний объясняется стремлением к неустойчивости движения в смазочной пленке. [26]
В этом пункте рассмотрены трп теоремы о неустойчивости движения, полученные Ляпуновым и Че-таевым. Исторически сначала были получены две теоремы Ляпунова. Эти теоремы были обобщены Четаевым, получившим теорему, которая нашла широкое применение при решении задачи об устойчивости в конкретных задачах механики, а также в теоретических исследованиях вопросов устойчивости. Мы сначала изложим теорему Четаева и затем выведем из нее обе теоремы Ляпунова о неустойчивости движении. [27]
В этом пункте рассмотрены три теоремы о неустойчивости движения, полученные Ляпуновым и Че-таевым. Исторически сначала были получены две теоремы Ляпунова. Эти теоремы были обобщены Четаевым, получившим теорему, которая нашла широкое применение при решении задачи об устойчивости в конкретных задачах механики, а также в теоретических исследованиях вопросов устойчивости. Мы сначала изложим теорему Четаева и затем выведем из нее обе теоремы Ляпунова о неустойчивости движения. [28]
Тогда будут выполнены все условия теоремы Н. Н. Красовского о неустойчивости движения § 2.4. Действительно, функция V может принимать положительные значения ( она определенно-положительна), а ее производная Р, согласно (2.58) и (2.60), положительна вне К и равна нулю на К. Следовательно, равновесное состояние системы I 0, и 0 неустойчиво. [29]
Доказательство теоремы следует теперь из теоремы Ляпунова о неустойчивости движения по уравнениям первого приближения ( см. § 4.3), и того обстоятельства, что свободный член aas характеристического уравнения не зависит от гироскопических сил. [30]
Страницы: 1 2 3 4