Соответствующий нуль

Cтраница 1

Соответствующие нули должны быть взяты из графика, полученного приравниванием выражения (18.22) нулю. [1]

Ввиду того что бесконечно удаленную точку можно считать лежащей на мнимой оси, на основании свойства 1 соответствующий нуль или полюс функции должен быть простым. [2]

Ввиду того что бесконечно удаленную точку можно считать лежащей на мшшой оси, на основании свойства 1 соответствующий нуль или полюс функции должен быть простым. [3]

Если хотя бы при одном из указанных значений е преобразованный многочлен удовлетворяет всем признакам устойчивости, то соответствующий нуль изображения лежит вне области расположения его полюсов и переходный процесс не будет монотонным. [4]

Лишь в частных случаях, как, например, для Ни, некоторые из полюсов могут сократиться с соответствующими нулями. [5]

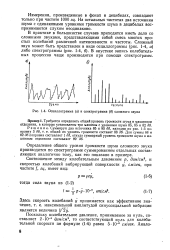Осциллограмма ( а и спектрограмма ( б сложного звука. [6]

Поскольку колебательное давление, принимаемое за нуль, составляет 2 - 10 - 4 дин / см2, то соответствующий нуль для колебательной скорости по формуле ( 1 - 6) равен 5 - 10-в см / сек. [7]

Сложение углов с помощью спиральной линейки. [8]

Чтобы из полученной суммы вычесть аргументы векторов, проходящих через нули разомкнутой системы, следует совместным вращением линейки с транспортиром направить верхнее ребро линейки через соответствующий нуль, а затем, придерживая пальцами транспортир, повернуть линейку в горизонтальное положение. [9]

В передаточных функциях Gw ( z) или Gn ( z) полюса полиномов A ( z) zd или А0 ( z) zd всегда компенсируются соответствующими нулями. Нули замкнутой системы определяются нулями объекта только для задающего входного сигнала. [10]

Интуитивно ясное утверждение, имеющееся в алгебраической геометрии, гласит, что, за исключением точек некоторого алгебраического множества, в См можно двигать точки аг - и соответствующие нули Р в S и строить изотопию окружающего многообразия S. [11]

Любая последовательность с длиной периода / я - 1 с k последовательными нулями приводит к последовательности с длиной периода т, если вписать в соответствующем месте нуль, как в упр. Обратно, мы можем начать с последовательности с длиной периода / п и вычеркнуть из нее соответствующий нуль, чтобы получить последовательности другого типа. [12]

Когда компенсационный регулятор GR ( z) с передаточной функцией (6.4) и объект Gpo ( z) объединены в замкнутую систему управления, то полюса и нули объекта сократятся с нулями и полюсами регулятора, если модель GP ( z) точно описывает объект. Однако используемые при проектировании модели GP ( z) B ( z) / A ( z) никогда точно не описывают динамику объекта, поэтому соответствующие нули и полюса сокращаются не точно, а только приближенно. Что касается полюсов ( корней полинома A ( z)) и нулей ( корней полинома B ( z)), которые расположены на z - плоскости внутри круга единичного радиуса, то неточность их сокращения, как правило, приводит лишь к незначительным отклонениям характеристик замкнутой системы от заданных. [13]

Пусть выполнены условия теоремы 3.8 и f ( z) - трансцендентная функция. Обозначим через п ( яг) число нулей / ( г), не являющихся ( являющихся) нулями / С 1 ( z), р - число полюсов / ( z), где всюду черта сверху означает, что соответствующие нули и полюсы считаются без учета их порядка. [14]

Можно описать эти дифференциальные сечения полюсными амплитудами, вставляя в вычеты без переворота спина у р - и со-полюсов произвольные нули ( см., например, [37]), но при этом возникают две сложности. Во-первых, в других процессах, таких, как п-р-у - о ( р-об-мен), я р - У р ( со - и Л2 - обмены) или ур-у я р ( р - и со-обмены), где р - и ш-полюса также связаны с каналом рр, не видно соответствующих нулей. Другими словами, этот вычет не факторизуется. Во-вторых, нуль в вычете полюса предполагает, что действительная и мнимая части амплитуды имеют совпадающие нули. В следующем разделе будет показано, что в действительности это не так. Поэтому ясно, что должны быть какие-то другие объяснения появления этих нулей, и опять разрезы кажутся наиболее правдоподобным объяснением ( см. разд. [15]

Страницы: 1 2