Определение - сходимость
Cтраница 3
Из этого определения и определения сходимости в пространстве Z следует, что обобщенные функции из Z - это такие аддитивные и однородные функционалы, определенные в пространстве Z, сужения которых на пространства Z ( а) являются линейными функционалами в этих нормированных пространствах. [31]
Пункт ( а) определения сходимости постулирует поведение алгоритма в такой ситуации, когда ему следует на некоторой итерации определить, что zh является подходящей точкой. [32]
Это вытекает непосредственно из определения сходимости в пространстве У. [33]
Необходимость условия вытекает непосредственно из определения сходимости интеграла (9.28): если интеграл (9.28) сходится, то последовательность ( 9.31) сходится и, следовательно, она ограничена. [34]
L) топология вводится посредством определения сходимости последовательностей. Вопрос о метризуемости классов ( L) тривиальным образом эквивалентен вопросу о метризуемости топологических пространств. [35]
Эффективность использования критерия сравнения для определения сходимости интеграла зависит, конечно, от запаса функций сравнения, о которых известно, сходится от них интеграл или расходится, и которые тем самым можно пытаться использовать для исследования сходимости данного интеграла с помощью признака сравнения. [36]
Однако применение критерия Коши для определения сходимости ряда затруднительно; его основное значение не прикладное, а теоретическое. [37]
Положим х 0 и проверим выполнение определения сходимости. [38]
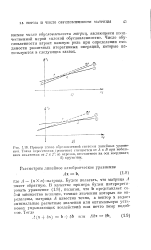 |
Пример плохо обусловленной спстемы линейных уравнений. Точка пересечения ( решение смещается от Л к В прп небольшом изменении от 2 к 2. а отрезка, отсекаемого на оси координат. [39] |
Число обусловленности играет важную роль при определении сходимости различных итеративных операций, которые используются в следующих главах. [40]
Последнее верно ввиду ( 17) и определения собственной сходимости. [41]
Утверждение ( 11) следует из сравнения определения сходимости по вероятности с критерием ( 5), а импликация ( 12) - из неравенства Чебышева. [42]
Утверждение ( 11) следует из сравнения определения сходимости по вероятности с критерием ( 5), а импликация ( 12) - из неравенства Чебышева. [43]
Утверждение ( И) следует из сравнения определения сходимости по вероятности с критерием ( 5), а импликация ( 12) - из неравенства Чебышева. [44]
Доказательство несложно и почти сразу же следует из определения сходимости в среднем. Однако обычная поточечная сходимость ( вообще говоря, неравномерная) не означает сходимости в среднем. [45]
Страницы: 1 2 3 4