Определение - сходимость
Cтраница 2
Для определения сходимости несобственных интегралов от разрывных функций и оценки их значений часто могут быть применены теоремы, аналогичные теоремам для оценки интегралов с бесконечными пределами. [16]
Для определения сходимости семейства сеточных функций к решению исходной задачи в пространстве vk сеточных функций необходимо задать расстояние между отдельными функциями как норму их разности. [17]
Для определения сходимости величин усилия волочения, найденных по формуле ( 23) и фактических, были произведены их замеры с помощью пружинных динамометров. [18]
Для определения сходимости семейства сеточных функций к решению исходной задачи в пространстве ( h v сеточных функций необходимо задать расстояние между отдельными функциями как норму их разности. [19]
Такому определению сходимости соответствует разновидность критерия Копш, называемая критерием Коши равномерной сходимости. [20]
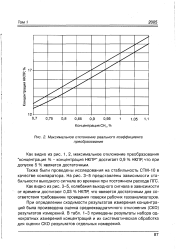 |
Максимальное отклонение реального коэффициента. [21] |
При определении сходимости результатов измерения концентраций была произведена оценка среднеквадратичного отклонения ( СКО) результатов измерений. В табл. 1 - 3 приведены результаты набора однократных измерений концентраций и их систематическая обработка для оценки СКО результатов отдельных измерений. [22]
С целью определения сходимости ряда ( 9) на машине было подсчитано значение потенциала в некоторых точках по направлению [111], учитывая различное число координационных сфер. Оказалось, что уже при числе ячеек 8 наступает насыщение и при дальнейшем увеличении числа координационных сфер значение потенциала не изменяется. [23]
С целью определения сходимости полученного теоретического решения и результатов опытного определения пределов выносливости по трещинообразованию и разрушению в зоне нераспространяющихся усталостных трещин на рис. 30 построены расчетные зависимости относительных пределов выносливости от теоретического коэффициента концентрации напряжений для мелкозернистой и крупнозернистой сталей. [24]
Если воспользоваться определениями сходимости и суммы ряда, то получим следующую теорему: для того чтобы ряд Тейлора функции f ( x) сходился к ней в некотором интервале, необходимо и достаточно, чтобы в рассматриваемом интервале стремился к нулю остаточный член этого ряда. [25]
При таком определении сходимости функционалов операции их сложения и умножения на число непрерывны ( это непосредственно следует из линейности функционалов и из свойств пределов числовых последовательностей), и, следовательно, справедливо следующее утверждение. [26]
При таком определении сходимости функционалов операции их сложения и умножения на число непрерывны ( это непосредственно следует из линейности функционалов и из свойств пределов числовых последовательностей), и, следовательно, если ввести понятие сходимости функционалов согласно определению 6, то будет справедливым следующее утверждение, которое мы сформулируем в виде отдельной леммы. [27]
Пусть дано некоторое определение сходимости и предела. [28]
Обратное очевидно из определения усиленной сходимости. [29]
Легко проверить, что определение сходимости, данное выше, удовлетворяет этому условию. [30]
Страницы: 1 2 3 4