Характеристический полином - система
Cтраница 2
В то же время легко проверить, что свойство устойчивости по переменной jt, пропадает при сколь угодно малых вариациях некоторых коэффициентов системы ( 91), например, коэффициента при х2 во втором уравнении, хотя все корни характеристического полинома системы ( 91) лежат далеко от мнимой оси. В монографии [10] данное явление объяснялось тем, что свойство асимптотической устойчивости по отношению к части переменных обладает повышенной чувствительностью по отношению к вариациям коэффициентов линейной системы ( [10], стр. [16]
Левая часть характеристического уравнения называется характеристическим полиномом. Характеристический полином системы ( с точностью до постоянного множителя и обозначений переменной) совпадает с ее собственным оператором и знаменателем ее передаточной функции. Характеристический полином замкнутой системы также равен ( при отрицательной обратной связи) сумме Р ( s) Q ( s) полиномов числителя и знаменателя передаточной функции W ( s) Р ( s) / Q ( s) разомкнутой системы. [17]
Начальные данные при t О для системы сравнения и системы ( 1), ( 2) одинаковы. В силу устойчивости характеристического полинома системы сравнения порожденная обратной связью ( 3) стратегия управления U. Кроме того, для неущербной процедуры генерирования тестового воздействия обеспечивается одинаковое качество управления в рандомизированной системе ( 1), ( 2) и системе сравнения в смысле заданного предельного квадратичного функционала. [18]
Мы видим теперь, как сложно восстановить истину в таком трудном деле, как расследование аварий. Остается несомненным одно - поскольку традиционные методы расчета устойчивости и ее сохранения при вариациях параметров основаны на исследовании характеристического полинома системы или матрицы ее коэффициентов при записи в форме Коши и не учитывают различия между преобразованиями, эквивалентными в классическом смысле и в расширенном, то традиционные методы не могут всегда, для всех систем давать правильные ответы. Следовательно, если в практику расчетов устойчивости не будут введены дополнительные проверки, описанные в уже упоминавшейся книге, изданной Ленинградским университетом в 1987 году [1] ( цифра, стоящая в квадратных скобках, означает номер в списке литературы в конце книги), то аварии будут возникать неизбежно. [19]
 |
Характеристики условно-устойчивой системы. [20] |
Хорошо видна роль амплитудных и фазовых преобразований, вносимых контуром, на устойчивость системы в целом. Изначальный смысл применения критерия Найквиста заключается не столько в констатации устойчивости, сколько в выявлении роли контура в перемещении корней характеристического полинома системы. [21]
 |
Характеристики условно-устойчивой системы. [22] |
Хорошо видна роль амплитудных и фазовых преобразований, вносимых контуром, на устойчивость системы в целом. Изначальный смысл применения критерия Найквиста заключается не столько в констатации устойчивости, сколько в выявлении рбли контура в перемещении корней характеристического полинома системы. [23]
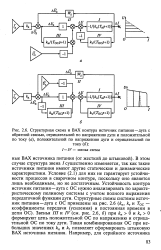 |
Структурная схема и ВАХ контура источник питания-дуга с обратной связью, отрицательной по напряжению дуги и положительной по току ( а, положительной по напряжению дуги и отрицательной по. [24] |
В этом случае структура звена / существенно изменяется, так как такие источники питания имеют другие статические и динамические характеристики. Условие (2.1) для них не гарантирует устойчивости процессов в сварочном контуре, поскольку оно является лишь необходимым, но не достаточным. Устойчивость контура источник питания-дуга с ОС нужно анализировать по характеристическому полиному системы с учетом полного выражения передаточной функции дуги. [25]
Теперь рассмотрим другой вопрос - о проверке устойчивости и запасов устойчивости в учебниках для университетов и технических университетов. В учебниках рекомендуется судить об устойчивости по корням характеристического полинома для линейных систем и по существованию ( или не существованию) функции Ляпунова для нелинейных систем. Если все корни характеристического полинома системы имеют отрицательные части; или если у системы существует функция Ляпунова, то такую систему учебники рекомендуют считать устойчивой. Уделяют слишком мало внимания тому, что параметры любой реальной системы почти никогда не могут быть известны идеально точно и почти никогда не могут быть идеально постоянными. Поэтому система, формально устойчивая при номинальных значениях параметров, но способная терять устойчивость при малых, неизбежных на практике отклонениях параметров от номинальных значений, ничуть не лучше ( и даже хуже) системы неустойчивой. Пригодной для практического использования может быть лишь система, имеющая ненулевой запас устойчивости, сохраняющая устойчивость при неизбежных вариациях параметров. Во многих учебниках о запасах устойчивости рекомендуют судить по расположению корней характеристического полинома на комплексной плоскости. Если все корни характеристического полинома лежат в левой полуплоскости комплексного переменного, далеко от мнимой оси, то система обладает конечным запасом устойчивости и пригодна для практического применения - такая рекомендация встречается во многих учебниках. На самом деле подобная рекомендация не верна и опасна. Примеры, приведенные в предыдущих главах, доказывают, что никакое исследование расположения корней характеристического полинома ( так же, как и исследование матрицы коэффициентов системы, записанной в нормальной форме Коши или существование функции Ляпунова) сами по себе ничего не говорят о запасах устойчивости. Для того чтобы быть уверенными в том, что проектируемая система имеет запас устойчивости и пригодна для практического применения, нужно обязательно провести дополнительные проверки, о которых было рассказано в предыдущих главах. О необходимости таких проверок, о ненадежности преобразований, эквивалентных в классическом смысле, но не в расширенном - надо обязательно ( хотя бы коротко) рассказать в ходе учебного процесса. [26]
Страницы: 1 2