Главный радиус - кривизна
Cтраница 2
Заменяя в уравнении Лапласа главные радиусы кривизны этими выражениями и учитывал зависимость капиллярного давления от вертикальной координаты z, получают дифференциальную форму уравнения Лапласа. Численное интегрирование такого дифференциального уравнения дает строгое математическое описание поверхности равновесной большой капли или пузырька, а также капиллярного мениска в поле силы тяжести. [16]
Для вытянутой эллипсоидальной оболочки главные радиусы кривизны являются наибольшими в зоне экватора / ( рис. 36), где и следует ожидать появления вмятин. [17]
Его применяют для определения главных радиусов кривизны и построения индикатрисы Дюпена рассматриваемой поверхности. [18]
Величины Rl и R2 представляют собой главные радиусы кривизны. Давление всегда больше в той среде, поверхность которой выпукла. [19]
Джеффрис и Хоксли [29] определяли главные радиусы кривизны капли воды на межфазной поверхности, проецируя фотографию капли, взятую из кадров скоростной киносъемки, на экран и анализируя затем ее профиль. [20]
Эта величина представляет собой разность главных радиусов кривизны эквивалентного зеркала, заменяющего собой брюстеровскую пластину и сферическое зеркало. [21]
H на единичной гиперсфере являются главными радиусами кривизны, то отсюда очевидным образом следует существование оценки для вторых производных Htj на единичной гиперсфере. Все они не превосходят диаметра гиперповерхности. Рассмотрим теперь оценку третьих производных. [22]
Радиусы Rm и Rt называют главными радиусами кривизны поверхности вращения. [23]
Как известно из дифференциальной геометрии, главные радиусы кривизны в данной точке поверхности-наибольший и наименьший радиусы кривизны среди всех нормальных сечений, проходящих через данную нормаль к поверхности. Взаимно перпендикулярные сечения, содержащие главные радиусы кривизны, называются главными плоскостями кривизны поверхности. [24]
Пусть далее Ri и R2 - главные радиусы кривизны в данной точке поверхности; мы будем считать RI и R2 положительными, если они направлены внутрь первой среды. [25]
Радиусы кривизны R1 и R2 называются главными радиусами кривизны нормальных сечений в рассматриваемой точке. Те два направления в касательной плоскости, которые их дают, называются главными направлениями. Кроме того в гиперболическом случае полезно отметить еще два направления в касательной плоскости, а именно - направления асимптот индикатрисы Дюпена. Для этих асимптотических направлений радиус-вектор индикатрисы равен бесконечности, и кривизна соответствующего нормального сечения в рассматриваемой точке равна нулю. [26]
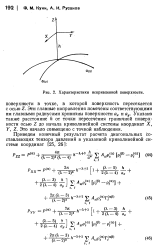 |
Характеристики искривленной поверхности. [27] |
Эти главные направления ломечены соответствующими им главными радиусами кривизны поверхности ах и ау. Указано также расстояние h от точки пересечения граничной поверхности осью Z до начала криволинейной системы координат X, Y, Z. Это начало совмещено с точкой наблюдения. [28]
Пусть далее RI и R % - главные радиусы кривизны в данной точке поверхности; мы будем считать RI и R % положительными, если они направлены внутрь первой среды. [29]
Для пологих оболочек можно считать, что главные радиусы кривизны RI и Л2 в пределах рассматриваемого участка пологой оболочки постоянны. [30]
Страницы: 1 2 3 4