Конечная разность

Cтраница 2

Метод конечных разностей стал сильным орудием решения задач для уравнений в частных производных с того момента, как Л ю-ст е р н и к о м [1,7] были использованы соображения, касающиеся поведения решения разностного уравнения в целом. Он одновременно рассматривает уравнение, которое нужно решать ( уравнение Лапласа), и разностное уравнение, которым оно приближенно заменяется. [16]

Метод конечных разностей, или, как его часто иначе называют, метод, сеток основан на замене решаемого дифференциального уравнения приближенным уравнением в конечных разностях. Такую замену можно рассматривать как замену дифференциального уравнения системой конечных уравнений с таким числом неизвестных, сколько значений функции подлежит определению. Известно несколько способов составления уравнения в конечных разностях, соответствующего рассматриваемому дифференциальному уравнению и его приближенно заменяющему. [17]

Метод конечных разностей базируется на возможности аппроксимации дифференциальных операторов, входящих в дифференциальное уравнение, более простыми локальными алгебраическими операторами, которые действуют в системе узлов, заранее выбранных в области. МГЭ в отличие от МКР и МКЭ, по сути, не рассматривает дифференциальные уравнения непосредственно в той форме, в которой они получены, а своим первым и основным шагом решения содержит преобразование исходных дифференциальных уравнений в эквивалентную систему интегральных уравнений. [18]

Метод конечных разностей. [19]

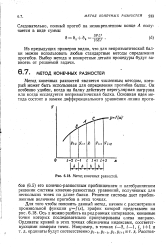
Метод конечных разностей является численным методом, который может быть использован для определения прогибов балок. Он особенно удобен, когда на балку действует нерегулярная нагрузка или когда исследуется непризматическая балка. [20]

Метод конечных разностей, который ранее использовался для определения прогибов балок, может быть примейен также и для исследования статически неопределимых балок. [21]

Схема к выводу уравнения в конечных разностях для одномерного безнапорного потока для оценки питания под - t 2JJ LLU. iJLJ. iJii LUJiJj земных вод. t 1 - - - - - - tZ2z2xt 2Zz. [22]

Метод конечных разностей основан на применении для гидродинамического анализа режима грунтовых вод уравнения неустановившейся фильтрации в конечных разностях, выведенного Г. Н. Каменским ( 1943) для профильного и планового потоков. [23]

Схема к расчету питания грунтовых вод путем анализа режима их уровня в одиночной скважине ( по Н. Н. Бин-деману, 1963. [24]

Метод конечных разностей лежит также в основе методов определения питания грунтовых вод по наблюдениям за режимом уровня в одиночной скважине. [25]

Метод конечных разностей отличается от аналитического тем, что для своего применения не требует аналитических решений дифференциальных уравнений, описывающих процесс неустановившегося движения во времени и в пространстве. Уравнения баланса воды в конечных разностях алгебраически преобразуются в простые расчетные формулы для определения гидрогеологических параметров, величин питания сверху и стока грунтовых вод исходя из данных о распределении напоров ( уровней) этих вод вдоль створов или по плановым группам наблюдательных скважин, а также по данным о режиме этих вод во времени и в пространстве. Граничные условия автоматически учитываются по данным о колебании уровней воды в скважинах, расположенных на границах потоков ( см. гл. [26]

Методы конечных разностей и аналитических решений уравнений неустановившегося движения используются в зависимости от сложности природных и техногенных условий, которые встречаются на конкретной местности. Для неоднородных в фильтрационном отношении водоносных толщ пород должен доминировать первый из этих методов. А для сравнительно однородных гидрогеологических условий и менее развитой сети скважин рекомендуется второй метод. [27]

Метод конечных разностей нашел широкое применение в практических расчетах тепловых устройств, тепловой режим которых меняется во времени. Примером является любая периодически работающая печь. [28]

Метод конечных разностей позволяет также осуществить расчет прогрева многослойных стен. Пример расчета прогрева двухслойной стенки приведен в § 3 гл. [29]

Методом конечных разностей ( МК Р) и элементов ( МКЭ) проведены расчеты напряженного состояния сопряжения металла шва и основного металла в сварных соединениях со смещением кромок. [30]

Страницы: 1 2 3 4