Квазиравновесное распределение
Cтраница 4
Однако, как уже отмечалось, само по себе распределение Qq ( t) еще не дает правильного описания неравновесных процессов, так как оно, вообще говоря, не удовлетворяет уравнению Лиувилля. Тем не менее, квазиравновесные распределения послужат в дальнейшем основой для построения решений уравнения Лиувилля, соответствующих сокращенному описанию макроскопических систем. Впервые идея использования квазиравновесных распределений в статистической механике была высказана Джейнсом [98, 99] и затем развивалась многими авторами. [46]
Построим сначала вспомогательное квазиравновесное распределение Qq ( q - p - t), рассматривая 8 ( а - а) как основную динамическую переменную, среднее значение которой характеризует неравновесное состояние системы. Как обычно, найдем квазиравновесное распределение из условия максимума информационной энтропии при заданном среднем значении ( 8 ( а - а) 1 и при сохранении нормировки. [47]
Подчеркнем, что эти решения удовлетворяют различным граничным условиям по времени. Запаздывающее решение стремится к квазиравновесному распределению при t - - оо, а опережающее решение - при t - оо. Опережающее решение дает не возрастание, а убывание энтропии системы [17] и в большинстве задач должно быть отброшено, как не имеющее физического смысла. [48]
Это название более удачное, чем принятое в русской литературе название квазиравновесный ансамбль, поскольку последнее вызывает необоснованные ассоциации с тепловым равновесием. Дело в том, что квазиравновесные распределения, которые будут вводиться в дальнейшем, могут описывать состояния, весьма далекие от равновесия. Хотя слово релевантный входит в наиболее полный словарь русского языка, оно практически не употребляется в физической литературе и выглядит несколько искусственным. Достойный русский эквивалент английскому термину relevant найти трудно. [49]
На первом этапе задача состоит в том, чтобы построить неравновесный статистический оператор, описывающий состояние системы. Как обычно, начнем с квазиравновесного распределения. Пусть Рт - набор базисных динамических переменных, включающий в себя операторы наблюдаемых потоков и, возможно, некоторые дополнительные переменные. [50]
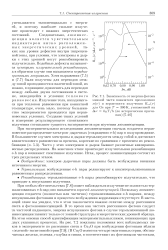 |
Зависимость от энергии фотона мнимой части показателя преломления f ( V и вероятности излучения Rvc ( для Ge при Т 300 К, умноженной на Ai / k & T / h ( по историческим причинам. [51] |
При экспериментальном исследовании люминесценции сначала создается неравновесное распределение электрон-дырочных ( сокращенно e - h) пар в полупроводнике. Часто у этих электронов и дырок бывают различные квазиравновесные распределения. На конечном этапе происходит излучательная рекомбинация e - h пар и возникает спонтанное излучение. Итак, процесс люминесценции состоит из трех раздельных этапов. [52]
В этом параграфе понятие квазиравновесного распределения иллюстрируется несколькими типичными примерами. Мы введем локально-равновесное распределение для классической жидкости, квазиравновесные распределения для классических и квантовых газов, диагональное квазиравновесное распределение для квантовых систем и квазиравновесное распределение для систем, состоящих из слабо взаимодействующих подсистем. [53]
Приступим теперь к выводу уравнений движения для приведенных матриц плотности. Как было показано в главе 3, выбор квазиравновесного распределения Qq ( i) является определяющим при решении цепочки уравнений для классических функций распределения. [54]
Страницы: 1 2 3 4