Псевдосфера

Cтраница 1

Псевдосфера построена Бельтрами в 1872 г. Параллельный перенос вектора по поверхности определен в 1917 г. Леви-Чивита, который с помощью параллельного обведения вектора по замкнутому контуру выразил кривизну поверхности. Теорема Леви-Чивита явилась обобщением теоремы Бонне ( 1867), в которой геодезический треугольник Гаусса заменен любой замкнутой кривой, а сумма его углов - интегралом от геодезической кривизны контура. [1]

Псевдосфера неограничена и, следовательно, на ней нельзя реализовать хаотическое движение: свободная частица, двигаясь по геодезическим, может уйти на бесконечность. Для того чтобы реализовалась хаотическая динамика, система должна быть компактной. Это очевидно для евклидовой плоскости, которую множеством способов можно разбить на многоугольники или даже, для простоты, на прямоугольники. Если противоположные стороны прямоугольника считать эквивалентными, мы получим движение в компактной системе. [2]

Псевдосферой называется поверхность, которая получается вращением трактрисы вокруг своей асимптоты. [3]

Рассмотрим псевдосферу мнимого радиуса. [4]

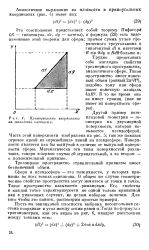Прямоугольные координаты на эвклидовой плоскости. [5]

Сфера и псевдосфера - это поверхности, у которых кривизна во всех точках одинакова. В общем же случае геометрические свойства пространства могут меняться от точки к точке. Такое пространство называется римановым. Его свойства в каждой точке характеризуются не одной только кривизной как в указанных случаях, но целым набором величин. Для того чтобы это понять, рассмотрим простые примеры. [6]

Итак, псевдосфера - это поверхность в обыкновенном реальном пространстве, на которой выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского. Стороны треугольника - это дуги псевдосферы, дающие кратчайшие расстояния между двумя ее точками и выполняющие ту же роль, которую выполняют прямые на плоскости; эти линии, называемые геодезическими, можно получить, зажав туго натянутую и натертую краской или мелом нить в вершинах треугольника. [7]

Рассмотрим на псевдосфере Бельтрами всевозможные круги одного и того же внутреннего радиуса г. Выяснить, какие из этих кругов конгруентны в R3, а какие нет. [8]

Очевидно, что псевдосфера нулевого радиуса совпадает с изотропным ( нулевым) конусом. [9]

Очевидно, что псевдосфера нулевого радиуса совпадает с изотропным конусом. [10]

К зывается радиусом псевдосферы. [11]

Распределение межуровневых расстояний в биллиарде Артина с периодическими граничными условиями, построенное в интервале импульсов 250 рп 300. Импульс рп связан с энергией соотношением Еп р - - 1 / 4. На вставке приведено то же распределение для интервала сравнительно малых значений импульса рп 100. [12]

Для дальнейшего обсуждения псевдосферу удобно преобразовать в полуплоскость Пуанкаре. [13]

Эта поверхность называется псевдосферой. [14]

Рассмотрим теперь стереографическую проекцию псевдосферы. Для простоты, мы рассматриваем только плоскость XOZ, так как все вычисления сохраняются при вращениях плоскости XOZ вокруг оси ОХ. [15]

Страницы: 1 2 3 4